Manacher马拉车算法是解决回文子串长度的算法,可以是时间复杂度为O(n),回文字符串就是正着读,反着读都一样的字符串,aba,abba。
由于回文串的长度可奇可偶, 为避免奇偶判断,Manacher的第一步预处理为在字符串的首尾和每个字符的间隙中都插入#,如#a#b#a#,#a#b#b#a#,这样转换后的字符串t恒为奇数,接下里加入一个辅助数组p,其中p[i]表示以t[i]字符为中心的回文子串的半径,若p[i]=1,那该回文子串就是t[i]本身。
# 1 # 2 # 2 # 1 # 2 # 2 #
1 2 1 2 5 2 1 6 1 2 3 2 1
由于第一个和最后一个字符都是#号,并且也需要搜索回文,为了防止越界,还需要在首尾加上非#号字符,实际操作时,我们只需要给开头加上非#号字符,结尾不用加的原因是字符串的结尾标识为\0,等于默认加过了,从上面可以看出p[i]-1正好为元字符串在i处的回文子串的长度,下面只要求出p数组中的最大值就行,新增两个辅助变量mx和id,其中id为最大回文子串的中心的位置,mx是回文串能延伸到的最右端的位置,这个算法的最核心的一行:
p[i] = mx>i ? min(p[2*id-1],mx-i) : 1;
如图j是i关于id的对称点:
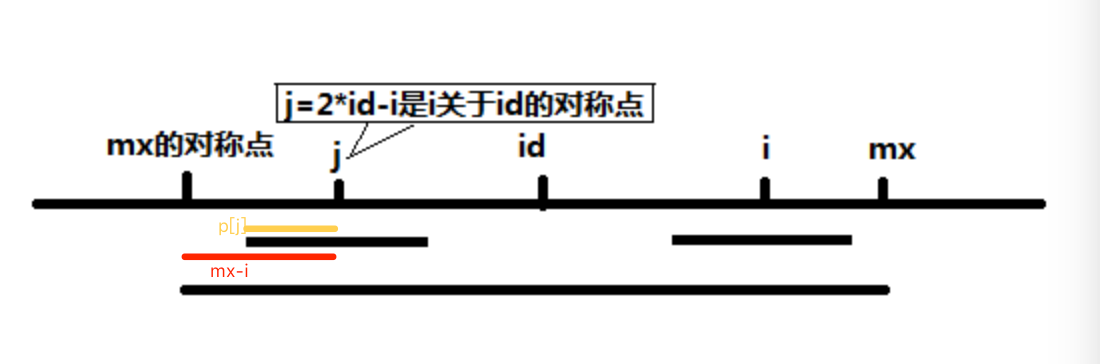
当mx>i时候p[i]=min(p[2*id-i],mx-i)=min(p[j],mx-i),为什么呢?
此时还需要分开讨论:
当mx-i>p[j]如上图,红色距离大于黄色距离。以j为中心的回文子串包含在id为中心的回文子串中。i和j对称,所以i为中心的回文子串也在id为中心的回文子串中,所以有p[i]=p[j]。
当mx-i>p[j]时候,j为中心的回文子串不一定全部包含在id为中心的回文子串中,基于对称性可知i为中心的回文子串最右端可能超出mx处,就是p[i]>=mx-i,如下图,绿色的部分是相同的。至于p[i]具体能在mx右边延伸到多远,就只能循环向右边扩展边比较,直至不为子回文串。
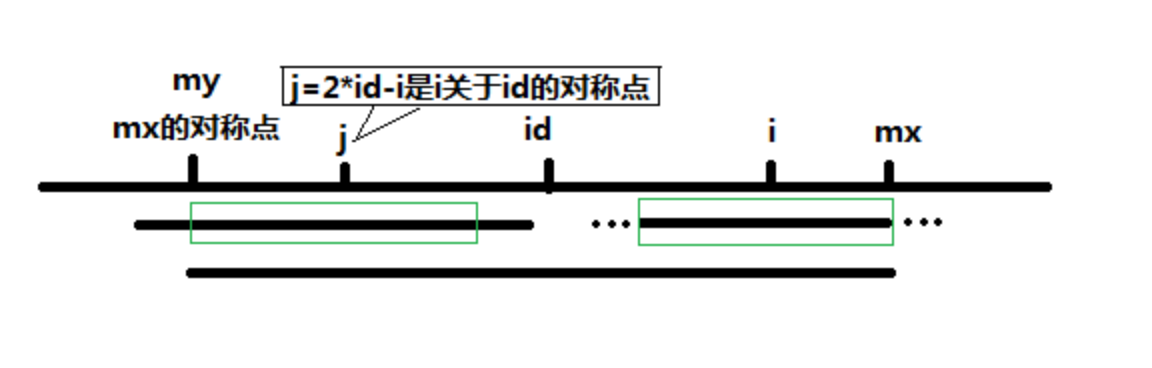
对于mx<=i的情况,i在mx的右边未知区域。无法对p[i]做更多的假设,只能p[i]=1,然后去虚幻向右比较扩展。
参考代码如下:
string manacher(const string &s) {
string t = "$#";
for (char i : s) {
t += i;
t += "#";
}
int len = t.size();
vector<int> p(len);
int mx = 0, id = 0, max_radius = 0, center = 0;
for (int i = 1; i < len; i++) {
p[i] = mx > i ? min(p[2 * id - i], mx - i) : 1;
// 向右匹配至不是子回文串
while (t[i + p[i]] == t[i - p[i]])
++p[i];
// 更新 mx,id
if (mx < i + p[i]) {
mx = i + p[i];
id = i;
}
// 记录全局最优解
if (max_radius < p[i]) {
max_radius = p[i];
center = i;
}
}
return s.substr((center - max_radius) / 2, max_radius - 1);
}